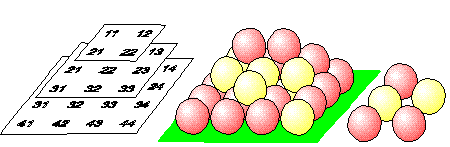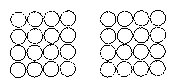ARCHÍV:1997. második forduló
ARCHÍV: 1998. második forduló
ARCHÍV: 1999. első forduló
ARCHÍV: 1999. második forduló
| (játékszabály) | |||||
|
|
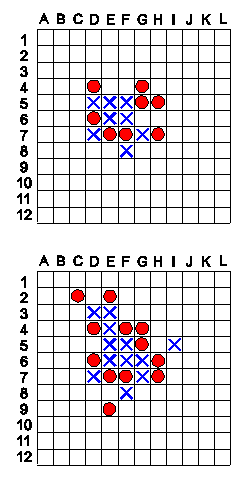
Mindkét állásban, mindkét játékos nyerhet, attól függően ki következik lépésre.
Összesen tehát két ábra, négy feladvány.
Mik a kulcslépések, és hányadik lépésében nyerhet O, ill. X, feltéve: hogy az ellenfél nem hibázik és nyerésre, ill. a lehető leghosszabb védekezésre törekedik. Részletes megoldás: a Magiszter magazin 1998. októberi számában (melybe egy "pici hiba is belecsúszott". Ennél a feladatnál ezt a hibát kérjük észrevenni!) |
||||
| (játékszabály) | |||||
|
|
Három kérdés, de csupán egyetlen hadállás, melyben már mindkét játékos csupán 3-3 bábujával küzd, az "ugrálós" játékszakaszban. 1. Ha sötét következik lépésre, akkor hányadik lépésével nyerhet, mi(k) a kulcslépés(ek) 2. Ha világos következik lépésre, akkor hányadik lépésével nyerhet, mi(k) a kulcslépés(ek)? 3. Valóságos partiban mikor/hogyan alakulhat ki ilyen állás, ha a végjátékban már egyik játékos sem hibázott? |
||||
| (játékszabály) | |||||
|
|
|
||||
|
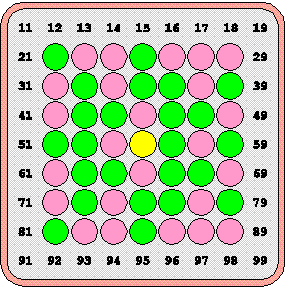
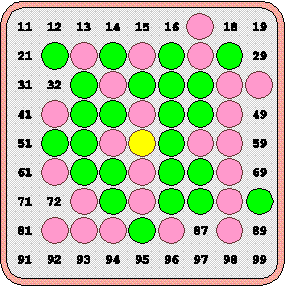
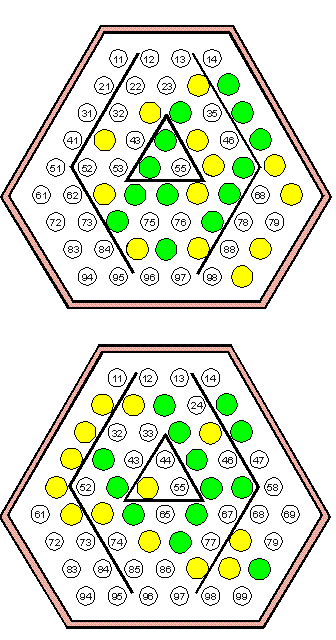
Mindkét állásban zöld következik és a rákövetkező lépésben biztosan nyer. Mi a kulcslépés, ha ellenfele nem vét hibát? A lépés leírásaként, annak a (lépést megelőzően üres) mezőnek a számát kell megadni, melyre az adott lépéssel golyó kerül. Így pl. a 21-es lépéskód, mindkét ábrán annyit jelent, hogy a táblán felülről számított második sorban álló golyókat egy pozícióval balra toltuk el. (Érdemes észrevenni, hogy ez a konvenció, akkor is egyértelmű, ha pl. a sarokmezőről van szó. Olyan állás ugyanis nem állhat elő, hogy a sarok üres, ha az alatta kezdődő oszlop is és a mellette kezdődő sor is 7 db golyót tartalmaz.) |
|||||
| (játékszabály) | |||||
|
|
két feladat, az első egy érdekes végjátszma, a második kicsit elméleti... |
||||
|
1. Az állásban világos lép (akinek csak 2 db golyója maradt a 3 db sötéttel szemben). Feltételezve, hogy mindkét játékos hibátlanul játszik, ki és hogyan nyeri a partit? (A golyóhelyek ábra szerinti számozását használva egyszerűsödik a megoldás leírása.) |
|||||
|
2. Színektől függetlenül, rakjunk fel a "földszintre" egyszer páros számban, egyszer páratlan számban annyi golyót, hogy a rákövetkező lépő már csak "lyukra tehessen"! |
|
||||
|
(Megfordítva: a földszinten összesen 4x4=16 db golyó fér el. Vegyünk le ezekből annyit, hogy mindegyik lehetséges kvadrátból, csak egyetlen golyó hiányozzon! A maradó golyók száma lehet páros is és páratlan is. Mindkét esetre rajzoljunk egy példát, úgy, hogy X-ek jelöljék az üres helyeket!) |
|||||
| (játékszabály) | |||||
|
|
Mindkét feladványban sötét lép és a rákövetkező lépésben biztosan nyer. Mi a kulcslépés, ha ellenfele nem követ el hibát? A lépéskód két számmal (kézenfekvően): 1.: a forgatás középpontjával azonos mező száma, 2.: az óramutató járásának irányában mért forgatási szög (,ill. az elforgatás mértéke: ?x60fok). |
||||
|
SOLITER ( játékszabály) |
|||||
|
Egy ábra, négy feladvány, mely valójában alig több egynél... |
|||||
|
|
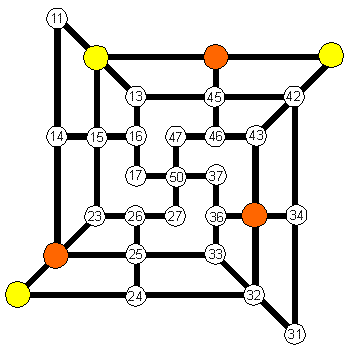
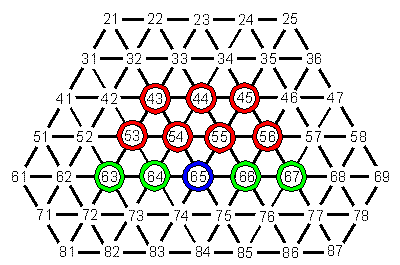
1. Az ábrán "felrakott" piros bábukat kell leütni, a soliterek szigorított szabályai szerint. (Ekkor, sem a zöldek sem a kék nincs a táblán! A szigorított szabály: egymást követően mindig más-más bábuval kell ütni.) |
||||
|
2. Mi az ütés-sorrend, ha a "remete" a kék színnel jelölt mezőre érkezik?
(Itt is a pirosakat kell leütni, de úgy, hogy az utolsó fennmaradó a kék jelű, 65. sz. mezőre kerül.)
3. A piros és a zöld bábukat mind le kell ütni. (A "remete" ekkor is a 65.sz. mezőre érkezzen!)
4. A fentiek (ugye) tényleg egyetlen feladványt alkotnak?
(A megoldások megfogalmazhatók külön-külön is, de valójában egyetlen feladat van: a 10 lépésből álló ütés-sorrend leírása.) |
|||||