A történet:
Latin négyzet-nek nevezik az olyan NxN-es négyzetet, aminek
minden sorában és oszlopában az 1-N számok egy-egy permutációja áll. Mivel
ezzel Euler foglalkozott sokat, vannak, aki tőle származtatják a sudoku-t.
A kiegészítő szabályt egy nyugdíjas amerikai építész, Howard Garns
találta ki, 1979-ben. Egy New York-i rejtvény újságban közölt néhány
rejtvényt "Number Place" néven. (Abban az évtizedben, mint Rubik a kockát,
és szintén építész!)
1984-ben a "Nikoli" nevű japán rejtvény társaság átvette a rejtvényt, és
a "sudoku" elnevezést adta neki. Japánban azóta töretlen a népszerűsége.
Több folyóirat csak ezzel foglalkozik, és azt állítják, hogy ők még mindig
kézzel csinálják a rejtvényeket.
2004 végén az új-zélandi származású, hong-kongi Wayne Gould ajánlotta a
számítógéppel készített rejtvényeit néhány neves angol újságnak, akik
"kipróbálták", és európai siker lett belőle, sőt Amerikába is visszatért a
játék.
Howard Garns nem érte meg a nagy sikert, egyik forrás szerint 1981-ben,
másik szerint 1989-ben meghalt.
A matematika:
Egy konkrét N-re nyilvánvalóan véges sok sudoku kitöltés létezik. A
4x4-es esetben ezeket programmal gyorsan elő lehet állítani, a 9x9-es
esetben (és a még nagyobb N-kre) számítógépnek is sok ez.
Bertram Felgenhauer és Frazer Jarvis sheffieldi matematikusok programmal
kiszámították, hogy 6670903752021072936960 különböző helyes (9x9-es) sudoku
kitöltés létezik. (>>)
Az alábbi - lényegesen különböző - transzformációkkal lehet jó sudoku
kitöltésből másik jót csinálni:
- A kilenc számjegy permutációja;
- A mátrix transzponálása (sor-oszlop csere);
- A sorok permutálása egy 3x3-as blokkon belül;
- Az oszlopok permutálása egy 3x3-as blokkon belül;
- A 3x3-as sor-blokkok permutálása;
- A 3x3-as oszlop-blokkok permutálása.
(A "lényegesen különböző"
azt jelenti, hogy pl. a forgatások, tükrözések az előzőkben benne vannak.)
Ha ezt figyelembe vesszük, akkor kiderül, hogy
5 472 730 538 lényegesen különböző kitöltés létezik. (>>)
Ezzel még el lesz egy darabig az emberiség.
Ez azért meglepő csökkenés, de vegyük figyelembe, hogy "a kilenc számjegy
permutációja" egyetlen kitöltésből 362879 (9!-1) különböző másikat
eredményez. És ezek mindegyikére végrehajthatók a fenti további műveletek!
Azt (még) nem tudjuk, hogy minimum hány négyzetnek kell kitöltve lenni
egy rejtvényben. Gordon Royle ausztrál matematikus már 35396 olyan
lényegesen különböző sudoku rejtvényt halmozott fel, amikben 17 mező van
kitöltve (a szám növekszik, a 2006. január 4-én érvényeset írtam ide). (>>) Olyan
rejtvényt még senki nem talált, amiben 17-nél kevesebb mező van kitöltve.
Rejtvény készítés:
Akik rejtvényt, sudoku készítő vagy megfejtő programot akarnak eladni,
azok algoritmust, forráskódot nem tesznek közhírré.
- Egy internetes fórumon
talált algoritmus vázlat mintájára készítettem az alábbit:
# készítek egy rejtvényt a következő módon:
üres táblát hozok létre
rejtveny_van_a_tablan="n"
lepes=0
while
rejtveny_van_a_tablan="n" && lepes<20000
egy véletlenszerűen választott üres mezőre teszek egy
véletlen számot az oda tehetők közül
ha a
kapott sudoku nem megoldható, leveszem
ha
megoldható és egyértelműen, akkor rejtveny_van_a_tablan="i"
# a "lepes"-t az utolsó két pont növeli (ld. alább)
# ha megoldható, de nem egyértelműen,
akkor folytatni kell a ciklust
# a kapott rejtvényt (ha
van) redukálom a következő módon:
if
rejtveny_van_a_tablan="i"
szam_db=`a
rejtvény kitöltött mezőinek a száma`
kiprobalva=0
egy_tomb-be beteszem az
összes szám helyét, kipróbálandó-ként
while kiprobalva<szam_db
egy véletlenszerűen választott, nem próbált számjegyet elhagyok
ha a kapott sudoku nem rejtvény,
visszateszem és kipróbáltnak adminisztrálom ("egy_tomb" és "kiprobalva"
módosul)
ha a kapott sudoku
rejtvény, újrainicializálom a mezőket (az "if" utáni 3 sort ismétlem)
A lépések száma (lepes) nem ciklusmenetenként eggyel nő, hanem attól
függően is, hogy a megoldás keresése hány lépésből áll. (Próbálkoztam
lépésszám korlátozás nélküli programmal is, elvileg az sem végtelen
ciklus, gyakorlatilag többször is annak tűnt.)
A fenti redukálás nem feltétlen találja meg az összes redukáltat,
hiszen ha az eredeti tábláról egy számjegy levehető, akkor a kapott
táblával folytatja, az eredetihez nem tér vissza.
Az algoritmus alapján készült awk program egy gyors PC-n közel
30 óra alatt 674 rejtvényt generált. (3 kivételével nem tölthetők ki
radírozás nélkül. Ez azt jelenti, hogy nincs minden lépésben egyértelműen
kitölthető mező, ha nem gondolkozunk több lépéssel előre. Más szóval: csak
három tölthető ki "visszalépés nélkül".) Ebben a tempóban
33497889728141811 év alatt lehetne az összes lehetséges sudoku kitöltéshez
egy-egy rejtvényt keresni. Érthető, hogy miért nem szólt még senki a
többieknek, hogy hagyják abba, mert ő mindet megtalálta.
- Gyorsabban lehet sok rejtvényt kapni úgy, hogy kitöltött sudoku-kat
generálok, aztán redukálom őket az előzőekben leírt módon.
Egy - scripttel generált - awk program
egy óra alatt ötmillió helyes sudoku kitöltést generált. (Elegendően sok
(csillagászati) idő alatt a script az összes sudoku-t előállítaná.)
Az első ötmillió kitöltés igen egyforma, mindegyik így kezdődik:

Ezt azzal tüntettem el, hogy a
feljebb leírt transzformációkat alkalmaztam a rejtvényekre,
véletlenszámokat használva közben. Az előző script bash változata
egy óra alatt csak százezer helyes sudokut állít elő. Viszont lehetőség
van arra, hogy a benne levő "for i.. in 1 2 3 4 5 6 7 8 9" parancsokban
(legalább az első néhányban) a számjegyeket véletlenszerűen permutálva,
több kisebb "csoportot" generáljunk az összes létező sudoku közül.
Ezzel a módszerrel óránként kb. 250 rejtvényt tudtam előállítani.
Összesen 5220-at generáltam. (143 kivételével ezek sem tölthetők ki
radírozás nélkül.)
A módszerrel visszalépés (backtrack) nélküli sudoku megfejtőt
készíthetünk úgy, hogy legenerálunk a rejtvény alapján egy hasonló,
megoldáskereső scriptet, az alábbi módosításokal:
- Előre kitöltött mezőre a megfelelő for ciklust és az azt
követő if sort egy értékadással helyettesítjük (pl. [3,5]=7
esetén i35=7.)
- Az if feltételek közé a megfelelő sor/oszlop/blokk "hátrébb
levő" kitöltött mezőitől való különbözést is be kell venni.
- Gyorsabb lesz a script, ha egy megtalált megoldás kiírása után
befejeződik (exit).
awk program generálását javaslom, a
bash változat túl lassú!
Ha a script azt számlálja csak
(legfeljebb a másodikig), hogy hány megoldást talált, akkor annak az
eldöntésére lesz jó, hogy megoldható-e, ill. (ha igen) rejtvény-e a
sudoku.
Önmagában is érdekes a 81-szeresen egymásba-skatulyázott, működő
for ciklus.
A generált rejtvények letölthetők.
Az első módszerrel készített 674 rejtvény a sudoku674 fájlban
van, a megfejtések (ugyanebben a sorrendben) a megfejtes674
fájlban. A nem_radiros674 fájlban a rejtvények olyan
bővítése van, ami radírozás nélkül megfejthető. Három hasonló fájl a második
módszerrel generált 5220 rejtvényt tartalmazza.
Sokkal több a lehetséges rejtvény, mint a lehetséges kitöltés, hiszen pl.
egy kitöltésből bármelyik számot elhagyva rejtvényt kapunk, továbbá a
kitöltés összes különböző "jó, de nem kész" állapota is rejtvény. Az
alábbiakban azt is látjuk majd, hogy egy rejtvénynek (és vele egy sudoku
kitöltésnek) lehet több redukáltja is.
Az általam generált (redukált) rejtvényekben 20-29 kitöltött mező van,
ennél több mező szokott lenni az emberi megfejtésre szánt - általában nem
redukált - rejtvényekben. Nem csak a megfejtő kedvéért, hanem a (japánok
által megkövetelt) szimmetria végett is tesznek a táblára redundáns
számjegyeket.
Matematikailag korrektnek a redukált rejtvény tűnik, az előbb említett
fórum a redukáltságot rejtvény szabálynak hiszi. Pedig nincs róla szó a
szabály leírásokban, mivel a megfejtés szempontjából érdektelen, hogy
redukált-e a rejtvény. Egy internetes lapon a géppel készített
rejtvényeket vádolják azzal, hogy redundánsak, pedig az alábbi példák azt
mutatják, hogy az embernek szántak azok, a "Nikoli" kézzel készített
rejtvényei is. A példák a legtöbbet hivatkozott sudoku lapokról, a
mai(2006.01.04) Metró újságból és a saját generálásból valók.
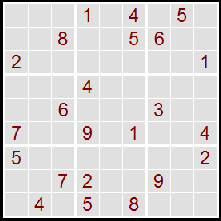
| Metro újság, 2006.01.04. Az "eredeti"-ek
radírozás nélkül kitölthetők. |
| eredeti |
egy redukált |
megfejtve |
 |
 |
 |
 |
 |
 |
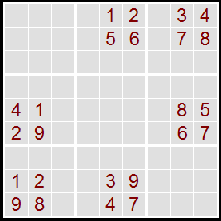
| Saját készítésű, radírozás nélkül
kitölthető |
| eredeti |
kitöltés: sor/oszlop/szám |
megfejtve |
 |
221 641 442 145 544 669 463 656 615 316 325
332 233 513 698 687 711 748 762 161 776 729 426 485 499 394 292 179
152 254 288 267 359 368 381 377 431 528 539 572 586 183 196 735 753
814 827 838 871 855 882 893 936 947 951 964 978 995 |
 |
4x4=2?
A 4x4-es sudokunak csak 288 különböző kitöltése van. A táblázatban ezt
igyekszem indokolni.
| sor |
kitöltés |
megjegyzés |
| 1 |
ABCD |
Az első sort 4!=24-féleképpen tölthetem ki, legyen ezek
egyike az ABCD |
| 2 |
CDAB
CDBA
DCAB
DCBA |
Mindegyik alá ennek a 4 második sornak az egyikét
tehetem (ez 24x4=96 lehetőség eddig) |
| 3 |
BA
BC
DA
BA
CA
CD |
Mindegyik alá az itt alatta levő három egyikét tehetem
a 3. sor első két mezőjére (Ez összesen 3x96=288
lehetőség) | Hiányzik még annak a belátása, hogy az
első 10 mezőt jól kitöltve rejtvényt kapok. Ez hosszadalmas,
eset-szétválasztásos okoskodás, a helyessége megkérdőjelezhető a hossza
miatt. Nem is túl érdekes, mert programmal egy pillanat alatt megkereshető
mind a 288
kitöltés.
Internetes fórumon
hasonló, ennyire sem részletezett okoskodás bizonyítja a 288-at.
Másik fórumon
azt látja be valaki, hogy csak két lényegesen különböző 4x4-es sudoku van.
Ez tkp. csak matematikailag érdekes, mert egy rejtvényfejtő szempontjából a
számok permutációja ugyanolyan, mint akármilyen egyéb csere-beréjük, ami
alapján azt hiheti a végén az ember, hogy bármilyen méretű sudokunak egy
független megoldása van, a többi ebből számok csereberéjével megkapható(!?).
4x4-es táblán igen egyszerű a minimumprobléma megoldása.
- 2 kitöltött mezős rejtvény nincs, mert a másik két szám cserélhetősége
miatt páros sok megoldása van.
- 3 kitöltött mező esetén a három számnak különbözőnek kell lennie
ugyanilyen okból. Ez viszont (a szimmetriákkal sem törődve), az 1,2,3
számoknak 16x15x14=3360 különböző elhelyezése, programmal gyorsan
generálható, és ellenőrízhető. Egyik sem rejtvény, vannak köztük olyanok,
amiknek nincs is megoldása.
 |
Pl. ennek nincs megoldása, mert a 12 alá a 34-et kellene tenni
valamilyen sorrendben, de a 3 már szerepel a
sorban. |
- 4 kitöltött mezős rejtvény sok van, közülük néhány itt
látható.
     
Az eddigiek alapján a 4x4-es sudoku valóban "gyerekjáték", de azért nem
annyira, hogy pl. a megoldásait az 1234 számjegyek összes 16-hosszúságú
ismétléses variációjából keressük, mert ezek száma
416=4 294 967 296, nem másodpercek alatt
előállítható.
Egyéb:
Vannak, akik a sudoku-t a Rubik kocka utódának tekintik. A
google keresőprogram közel 19 millió weblapot talál a "sudoku" szó
beírására.
Rengetegen próbálnak pénzt csinálni abból, hogy rejtvényeket vagy ahhoz
kapcsolódó programokat adnak el. Gordon Royle 17-esein kívül nem találtam
nagyobb mennyiségű, ingyen letölthető sudokut.
A rejtvényeket nehézség szerint kategorizálják. Ez összefügg azzal is,
hogy hány négyzet van előre kitöltve, de inkább azzal, hogy hány négyzetnek
egyértelmű a kitöltése. Matematikailag pontos definíciókat is ki lehetne
erre találni, amik nem biztos, hogy a kitöltők véleményével egyeznének.
Készítenek mindenféle egyéb méretű és beosztású sudoku rejtvényeket. Pl:
- 9x9-esnél nagyobbat, pl. 12x12-est;
- 6x6-ost, 2x3-as blokkokkal (gyerekeknek);
- Olyat, ahol a blokkok nem téglalap alakúak. (>>)
Két, forrásnyelven elérhető, rejtvény fejtő programot letöltöttem az
internetről. Egyik perl-ben a másik PL-SQL-ben (Oracle)
íródott. Egyszerű rejtvényt mindegyik gyorsabban fejtett meg, mint az
általam awk-ban írt program, de Gordon Royle első "17-es"-én
mindegyik elbukott. (A perl program azt állítja, hogy nem
megoldható, a másik pedig gyorsan ad egy egészen hibás megoldást.)
A 9x9-es sudoku-hoz kapcsolódó számok sok esetben óriásiak.
Gordon
Royle első "17-es"-éből levettem egy számot, és megkerestem a megoldásait.
265244 megoldása van! (Ekkor lemondtam arról a tervről, hogy Royle
17-eseinek a redukáltjaként keressek 16-ost. Ha ilyen egyszerűen található
lenne, ő már biztos talált volna.)
Az összes megoldás (81+1 jel
hosszúságú sorban tárolva egyet) 509446587102234 GB lenne tömörítés nélkül!
Az összes lényegesen különböző megoldás viszont csak 418 GB.
Az a hit (Nikoli), hogy kézzel nagyobb szellemi élvezetet nyújtó
rejtvények készíthetők, annyira sem megalapozott, mint évtizedekkel ezelőtt
az a vélemény, hogy programok legfeljebb "mesterjelölt" szinten tudnak majd
sakkozni. Redukált rejtvényt programmal is lehet úgy bővíteni, hogy
- szimmetrikus legyen
- ne legyen túl könnyen megfejthető
- ne legyen túl nehezen megfejthető
- ...
A "ne túl könnyen, ne túl nehezen" kritériumai akár a
legjobbnak tartott kézi rejtvények elemzésével is kialakíthatók. Úgy tűnik,
hogy kb. is jelentik, hogy vagy (teljesen) radírozás nélkül kitölthető
legyen a rejtvény, vagy csak pár lépést kelljen előre gondolkozni egy mező
egyértelmű kitöltéséhez (vagyis ténylegesen ilyenkor se kelljen radírozni).
Végül néhány érdekes sudoku Gordon Royle gyüjteményéből (egyik sem
tölthető ki radírozás nélkül). (>>)
| eredeti |
egy redukált |
megfejtve |
 |
az első 17-es;
nem redukálható |
 |
 |
17-es, 3 üres sorral;
nem redukálható |
 |
 |
szimmetrikus 18-as;
nem redukálható |
 |
 |
 |
 |
 |
négyzetmintás;
nem redukálható |
 |
 |
X-lábú;
nem redukálható |
 |
Végül egy magyar lap a témához: http://sudoku.lap.hu/
|