|
A hetvenes évek elején, amikor a számítógépes vírusok feltűnése még nem volt ilyen mindennapos jelenség, volt egy másik, a számítógépek tulajdonosait fenyegető járvány. Ez, az emberi agyat használta átmeneti gazdának. A számítógépes életjáték, amelyet széles körben először Martin Gardner ismertetett legendás hírű rovatában a Scientific America című folyóiratban, gyorsabban terjedt, mit a spanyolnátha. A bankok és biztosító társaságok azt vették észre, hogy számítógépidejük nagy részével nem tudnak elszámolni. Sok programozó a játék rabja lett és ezzel töltötte munkaideje nagy részét, állandó készenlétben arra, hogy -ha a főnök netán arra sétálna- az ESC gombot megnyomva, kitörölje az életjáték árulkodó jeleit…
John Horton Conway, egy kiemelkedően termékeny cambridbe-i matematikus alkotta életjáték valami különleges dolog volt. Nem kétszemélyes, mint a dáma, vagy a sakk, és nem is pasziánsz. Egy személytelen játék. Egyetlen számítógép elég hozzá. Az emberi résztvevőnek a játék megfigyelésén kívül csak egyetlen dolgot kell tennie: meghatározni a kiindulási pozíciót. A többi már magától következik be.
A játéktér egy végtelen nagy sakktábla, melyen minden négyzet alapú cellának nyolc szomszédja van.
A szabályok egyszerűek. Ha egy cella üres, akkor a következő nemzedékben is üres marad, kivéve, ha pontosan három szomszédos cella foglalt, -ez utóbbi esetben a következő nemzedékben foglalt lesz-. Fordítva, ha egy cella már foglalt, akkor foglalt marad a következő nemzedékben is, ha két, vagy három szomszédja foglalt, -egyébként üres lesz-. A foglalt és üres helyett azt is mondhatjuk, hogy be, vagy kikapcsolt állapotú, azaz élő, vagy holt.
Összefoglalva: ahhoz, hogy születés történjen, három szomszédnak kell életben lennie, ha több van, akkor a cella ("túlnépesedés miatt"), ha kevesebb, akkor ("elszigeteltség miatt") kihal.
Ilyen módon változik az élő cellák populációja nemzedékről nemzedékre. A cellák sorsa lépésről lépésre pontosan meghatározott, a végtelenségig. Jövőjüket a kiindulási állapot teljes egészében tartalmazza, ettől semmiféle eltérés nem lehetséges…
A kiindulási állapottól függően lesznek kihaló, oszcilláló, pulzáló, alakjukat időnként visszanyerő, vándorló,
a végtelenségi növekedő, stb. formációk… Ez utóbbiak létezésének belátásához fűződik a "világ legolcsóbban
vásárolt számítógépidejének sztorija": Conway 50 dollárt ígért egy bizonyítottan végtelenül növekedő formáció
kiindulási állapotáért… és a számítógépek egyetemeken, bankokban, hivatalokban, stb. beindultak… A megoldás egyébként
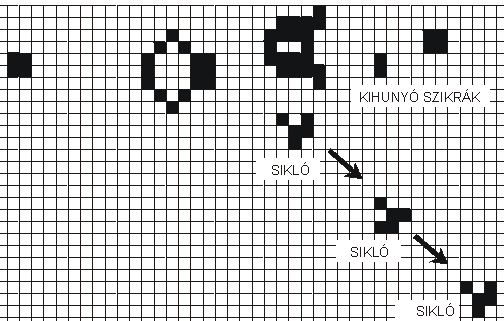
igazolta Conway sejtését, hogy a bizonyításhoz pl. egy "siklógyú" található, olyan oszcillátorként pulzáló alakzat, mely
periodikusan visszatérő, néhánygenerációnyi ütemben újra és újra, egy-egy egyenes vonalban vándorló alakzatot "lövel"
ki magából…
Ez utóbbit láthatod a képen, ill. a fenti JAVA mintabeállításban.
Igazán nem mondhatni táblajátéknak! Ám korábban, még a commodore-s időszakban
magam is írtam néhány változatot Conway életjátékára. Döbbenetes élmény a "teremtés"! Megalkotod
a születés és a halálozás szabályait, megadod az induló populációt, majd hátradőlve foteledben
szemléled hogyan folyik le az általad teremtett világ "történelme". Vajon sikerült-e örökéletű és folyton
változó világot teremtened, vagy néhány generáció után leáll a fejlődése, netán kihal, vagy
születnek-e belőle új világok, saját szabályokkal és ezek túlélik-e az őket szülő világot, egymással
versenyezve lesznek-e túlélők, vagy néhányukból egy újabb világ születik?
Beszélgettem néhány ismerősömmel. Némelyike
szinte indulatosan is hangot adva véleményének, nem értette mi ebben az életjátékban
az érdekes. Különösebb győzködés nélkül abban maradtunk:
"Nem vagyunk egyformák. Ha például húzunk egy függőleges vonalat és a vonal egyik oldalára helyezzük a azokat
, akiket lenyűgöz Conway életjátéka, a másikra pedig azokat akiket ez hidegen hagy, akkor az
így szétválasztott két csoportra megállapíthatunk nagy valószínűséggel teljesülő általános
jellemzőket: pl. az egyik kedvel valamilyen táblás játékot... Azt viszont ne firtassuk, hogyha ezt
a bizonyos vonalat vízszintesen húzzuk meg, akkor melyik csoportot ábrázolnánk vonal felett és melyiket
a vonal alatt." /Nagylaci/
|