|

|

|
|
|
|
|
"Újszülöttnek minden vicc új."
Újszülöttnek?
Ezer látogatóm közül tánha egy látta már valahol, pedig szinte nincs is olyan logikai játékokat kínáló játszóház,
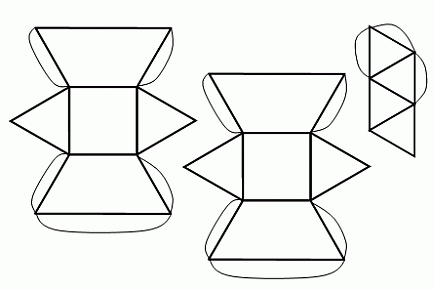
ahonnan hiányozna ez a két félből összerakható:
'tetraeder'
A képrekattal megnyíló doc-fájlt ajánlom klubvezetőknek, játszóházi animátoroknak,
különösen pedagógusoknak.
A lenti beszámolót azoknak, akik
már ismerik, de a talány feladásán túl, nem gondolták át a lehetőségeit...
|


|
Az alábbi móka, eddig még mindig működött a játszóházaimon*
(* lassan abbahagyom, "ellőhetők a poénok", hiszen továbbgondolva többeknek tanulságos lehet):
A "kinél van stopper?" felkiáltásra jelentkezők egyike lesz az egyik versenybíró, (igyekszem olyat
választani, aki becsühetően ritkán -netán még soha sem- jutott irányító szerephez).
A hangoskodásra gyülekezőknek megmutatom a két testet és a kicsinyitett méretű kirakandó mintát, az alábbi versenyt hirdetve (hangosan, hogy a további érdeklődökhöz is eljusson):
"A versenyzők körbeállják az éppen soros próbálkozót, vele együtt gondolkodhatnak, de tilos hangoskodni, vagy segítő-félrevezető utasítást adni... Mindenki 1-1 percig próbálkozhat..."
Ajándékot ígérek a versenybíróknak és a legrövidebb idő alatt kirakónak, majd azt választom ki másik versenybírónak, akiből kinézhető, hogy a legesélyesebb lenne a győzelemre.
Amikor minden érdeklődö összegyűlt, megismétlem a szabályokat:
"A soron következő leül és a stopperos versenybíró, indítva az időmérést, a két kezébe adja az elemeket. Ha 1 percen belül megoldja, akkor a másik versenybíró feljegyzi a nevét és a megoldási időt. Sikertelen a próbálkozás, ha letelt az 1 perc, feláll és leül a következő..."
Megismétlem, hogy nem tilos lesni-körbeállni, de aki hangoskodik, vagy beledumál, azt a versenybírók kizárják. A feladat ismétléseként: "Az egyiptomi piramisok négyzet alakú gúlák, milliónyi kőből..., ez itt csupán 2 db kő és háromszögalapú olyan gúlát lehet belőlük kirakni, minta kicsinyített minta, aminek minden lapja szabályos háromszög...,( ugye ez a legegyszerűbb platoni test, a tetraeder..., azaz négy egymással egybevágó lapú...)"
Ezután magára hagyható a csoport, mindaddig, amíg valamennyi benevező sorra nem került..
(Eddig még, mindig elég rövid volt az 1 perc ahhoz, hogy ne akadjon sikeres megoldó.)
A kudarcos, de tovább drukkoló kitartókhoz visszatérve, "a nincs is megoldás" reklamációra kiválasztom a legkevésbé gyakorlottnak ígérkezőt és leültetve, előbb a mintát adom a kezébe: "Számold meg, hogy hány hegyes csúcsa van a tetraedernek!"
(Gyakorta háromról indulunk, aztán egyetértőleg megállapodunk négyben.)
"Tedd le az asztalra és nézd meg jól, hol vannak ezek a csúcsok!"
Miután leellenőriztük, hogy 3 db csúcs az asztalon van 1 db meg fenn felette, a kezébe adom az egyik elemet:
"Ennek hány olyan hegyes csúcsa van, mint amit a mintán számoltunk?"
(Némi elemzéssel/értelmezéssel megegyezünk, hogy 2 db, mert a többi nem annyira hegyes.)
"Nos, a másik ugyanilyen elemen hány hegyes csúcs van?"
(A válasz mindig helyes, hiszen mint két tojás úgy azonos a két elem.)
|
|
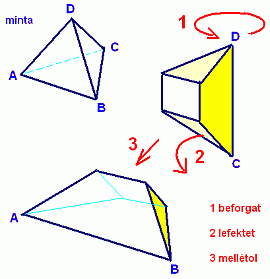
Még mindig csak az egyik van a kezében, amit lerakatok az asztalra és megszámoljuk, hogy a kirakandó tetraedernek már két hegyes csúcsa ott is van az asztalon, amiket összehasonlítva a mintával, megtervezzük a másik két csúcs helyét és csak ezek után, ekkor adom a kezébe a másik elemet:
"A lerakotthoz most már ne nyúlj hozzá, de úgy rakd-forgasd mellé ezt a másikat, ahogy megbeszéltük: az egyik hegyes csúcsa az asztalon, a másik hegyes pedig felette fenn legyen!"
5-10 másodpercen belül sikerül, a többiek is kézről-kézre adják... és közben végighallgatják a tanulságot:
a minta szerinti építkezésről, a részek összehasonlí-tásáról, azonosításról, egyező tulajdonságú pontokról, hozzáfűzhető szimmetria, tükörkép, meg még amihez van türelmük...
| 
|
|
|