Hanoi Torony

Többen kérték, feltettem hát egyet, bár: nem maga a megoldás a feladvány, hanem a legkevesebb lépésszám kiszámítása.
Ehhez persze jó,
ha akad egy szemléltető eszköz.
(lásd lent a lyukas korongokat a rudakra)


Ez a változat még működik:
Egyenként átrakosgatni úgy, hogy közben soha nem kerülhet nagyobb kisebbre... Voltaképpen egyetlen kérdés:
Mi az első lépés?



Hány lépésből oldható meg pl. egy ilyen, 10-korongból álló átrakosgatós?

Vegyük észre, hogy a B és a C elnevezés felcserélhető, azaz A-ról B-re átrakni, vagy A-ról C-re átrakni ugyanannyi lépés.
Az ábráról egyértelmű, hogy 1. a zöld keretbe foglalt 9 db korongot mind át kell pakolni egy másik rúdra ahhoz, hogy

2.a célrúd aljára áttehessük az 10. legnagyobb korongot, majd

3. ezt követően, a célrúdra átpakolni még a többit is, pontosan ugyanaz a feladat (és lépésszám), mint amit az 1. fázis alatt elvégeztünk.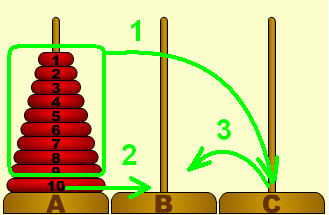
A 10 db korong átpakolása tehát: eggyel több lépésben oldható meg, mint 9 db korong esetéhez szükséges kétszerese. A 9 db-hoz pedig kétszer annyi + még egy lépés kell, mint a 8 db-éhoz… és így tovább visszafelé...,
azaz általánosan megállapítható: Egy adott számú korongot tartalmazó csomag átrakásának lépésszáma mindig eggyel több, mint a nála eggyel kevesebb korongot tartalmazó csomag átrakásához szükséges kétszerese.

X(N) = 2 x X(N-1)+1

(Az ilyen képletformát, amelyben egy sorozat két egymást követő, de különben tetszőleges tagjára adunk meg egy összefüggést, a matematikában „rekurzív” képzésnek nevezzük.) A lépés-számot tehát a nélkül is meghatározhatjuk, hogy megpróbáltuk volna tényleges rakosgatásokkal: 1 , 2 , 3 , ... (korongok száma)

1 , 3 , 7 , ... (minimális lépés-szám)

2 , 4 , 8 , ... (ezek pedig 2 növekvő hatványai) Ezt pedig, még végig sem kell számolgatnunk, mert felsejlik, hogy a középső számsor értékei eggyel kisebbek, mint az emlékeztetőül alájuk írt harmadik számsor, azaz 2 növekvő hatványai.

Ha ez így van, akkor a 10-korongos változat megoldásához:

2*10 -1 lépés kell, ami több, mint 1.000 (!)

Hogy biztosan nem tévedünk és a „kettő-hatványos” sejtésünk nemcsak az első néhány esetre igaz, azt persze be is kell bizonyítanunk.

Azért is, hogy ne essünk egy megalapozatlan általánosítás csapdájába!
Jellemző példa:
Ha egy mérnök azt a feladatot kapja, hogy sorolja fel a prímszámokat, akkor előbb példákat keres:
1 ? az prímszám;
2 ? az is prímszám;
3 ? úgyszintén, hiszen
ez sem osztható önmagán és 1-en kívül mással.

A példák alapján aztán következtet: "minden szám prímszám!"
:-)

Tételezzük fel, hogy egy K. elemre igaz ez a számolás, azaz: T(K)=2*K-1!
Ekkor viszont biztosan igaz lesz a következő elemre is, hiszen ha a rekurzív formulánkba N=K+1-et helyettesítünk, akkor ugyanezt az eredményt kapjuk: T(K+1)=2x T(K) +1= 2 x (2*K-1) +1= 2*(K+1)-1

(Ezt az utóbbi bizonyítási módszert a matematikában „teljes indukció”-nak hívják: Bizonyítsd be az elsőre, majd nézd meg, hogyha igaz egy tetszőleges K-adikra, akkor a K+1-dikre is igaz lesz!)