Pentominó feladványok
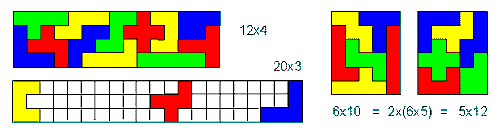
Többnyire logikai játékként minősítik a kirakós pentominókat. A 12x5=60 egység-négyzetnyi terület, téglalapos elrendezésben,
3x20, 4x15, 5x12 és 6x10 méretű lehet. Valamennyi ki is rakható a teljes készlet
pentominóból. |

|
 |
Négyzetes elrendezésben a 12x5=60 területegységhez legközelebb a 8 egység
oldalú áll: 8x8=64. Ez is lefedhető az alapkészlettel (kb.100000 különböző megoldásban) persze
úgy, hogy 4 egységnyi területrész mindig üres marad. |
|
Ha például olyan megoldásokat keresünk, melyben az "üres négyes" középen van, akkor (a tükörképek és szimmetriák "kiszűrése" után is) 65 különbözőt találhatunk. Érdekes, hogy mind a 65-ben valahová a négyzet szélére fog kerülni a hosszú (I) elem. Az is bebizonyítható (pl. néhány próbálkozással), hogy az üres négyes bárhol kiadódhat a 8x8-as táblán. Kicsiknek, a pentominókkal ismerkedőknek, kezdésként biztosan sikerélményt nyújt a legkönnyebben megoldható feladat: úgy kitölteni a 8x8-as táblát, hogy a négy kicsi "üres" egységet a legvégén, a lyukak betömésére használhatják fel, függetlenül a szimmetriáktól. Ezt követően jöhetnek a nehezebbek: előre felrakott kis négyzetek... majd a többi téglalap... Utána pedig pl. a háromszoros formák... 
Szabálytalan formákkal próbálkozva, nem csupán kézenfekvően kínálkozó feladat, de meg is oldható mindegyik pentominó háromszoros méretben történő előállítása a többiből. Mivel 3x3x5=45, 60-45=15 és 15/5=3, három pentominó mindig ki fog maradni. Ám, egy-egy alakzat más és más módon történő lefedésekor, másik három fog kimaradni. (Ha 9 készlet pentominót készítenénk, pl. kartonlapból, azokból pontosan kialakítható lenne mindegyik pentominó háromszorosra nagyított mása, majd ezekből a háromszoros blokkokból kirakott, óriás "3x20"-as, vagy "6x10"-es téglalap, érdekes-tetszetős, akár falra akasztható intarziaképet eredményezne...) 
Sikerrel próbálkozhatunk a háromszög elrendezéssel is (ekkor, 1 db fog kimaradni, más elrendezésben másik darab), és persze próbálkozhatunk a magunk kitalálta különböző formák kirakásával is...
Hamarosan bejuthatunk a feladványkészítők táborába... Nem lesz könnyű újabb, még sehol sem közölt feladványhoz jutni. Sok-sok elme "agyal" ezeken immár félszáz éve, időnként "kincset" is találva. Ezekből néhány igazi csemege: 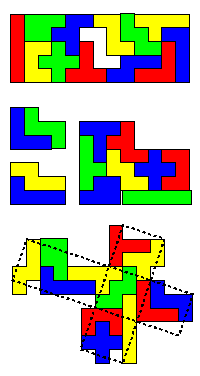
a "lyukas 5x13-asok" (P.J. Slate) Az 5x13=65 területegység pont egy pentominónyival nagyobb, mint az összes pentominó által lefedhető terület. Rakjuk ki úgy az 5x13-ast, hogy az üres rész középre kerüljön és alakja egyezzen meg egy előre kiválasztott pentominó alakjával! a "kétféle kétszerezések" feladványai (H. Brueggemann ) 2 db pentominóból rakjunk ki egy alakzatot, majd keressünk további kettőt, melyből ugyanezen forma kialakítható! A maradó 8 db pentominóból alakítsuk ki az előbbi alakzatok kétszeresét!
a "kockapalást" (H.D. Benjamin) A 12 db pentominó pont lefedi egy négyzetgyök tíz egységnyi élű kocka kiterített palástját. Meggyőződhetünk róla "nézegetéssel" is, és úgy is, ha papírlapra rajzoljuk, kivágjuk és a vékonyan rajzolt vonalak mentén hajtogatjuk... |